Random numbers are very important as they are used to generate cryptographic keys used for encrypting data. If the random numbers are compromised, keys can be predictable and hence compromised. The security of our products relies on good cryptographic keys. Over the last few weeks I’ve received several inquiries as to the security of Vormetric’s random number generation, so I thought I’d write a technical blog post to address the matter.
Random numbers might seem to be an obscure niche of security products, but they have certainly become a hot topic in crypto circles recently, thanks to Edward Snowden and the controversy around NSA building back doors into products. Back in September I wrote about the “DUAL_EC_DRBG” random number generator and the backdoor it contained. Just recently my colleague Andy Kicklighter wrote a great piece on how the NSA paid RSA to make DUAL_EC_DRBG the default random number generator in their BSafe library – and hence give it a backdoor into all products that use it.
I’d like to take this blog post to describe all the nuts and bolts of what we do and provide a great degree of transparency into how our products use random numbers to generate encryption keys. This should help some concerned and curious customers. I’ll start with the original sources of entropy and then journey upwards through the various layers of post-processing up to where it is used.
There are really two different topics to discuss when you’re talking about random numbers on computers: entropy and Pseudo Random Number Generators (PRNGs). (PRNGs are also called “Deterministic Random Bit Generators (DRBGs), mostly by NIST.)
- Entropy is data that comes from a truly unpredictable source – one not tied to a computer algorithm or anything that is deterministic or could be guessed. Good sources of entropy are surprisingly difficult for computers to acquire. A computer is designed in every other way to be a predictable, logical machine that will always give you the same answer when you ask it the same question. This is exactly the opposite property that you want in a good source of entropy. Fortunately there are a few places where entropy exists on a modern computer. One is the hard drive. It is a mechanical device with a spinning platter and a mechanical arm – both of which can lead to unpredictable variations over time. The biggest problem with this source of entropy is that it comes rather slowly – too slowly for many applications.
- PRNGs, on the other hand, take a “seed” value and create a stream of numbers that look really random, but are all based from that seed number. Beyond making random-looking numbers, a good PRNG is resistant to guesses about previous and future output. However, if the seed number is guessed correctly, the entire stream of numbers can be known. For example, I can seed a PRNG with a “0” and have it produce a nice long string of random-looking numbers – but I can also restart that PRNG, give it a seed of “0”, and it’ll produce the exact same stream of numbers again.
This is where combining a good source of entropy with a PRNG comes into play. The entropy source is used as the seed value to the PRNG, and the entropy source can periodically be used to “re-seed” the PRNG. Assuming the PRNG is strong, it can quickly produce random output, and because it uses a good source of entropy, the seed is difficult to guess.
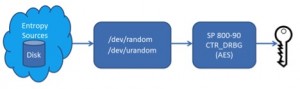
With that background in mind, let’s follow the bits in our Data Security Manager (DSM) as they start as entropy and end as a key. We start at the lowest level – the Linux kernel. It provides the “Linux Pseudorandom Number Generator”, or LPNG. The LPNG supplies two sources of random numbers through devices named /dev/random and /dev/urandom.
The LPNG looks like this:
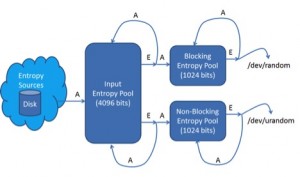
The lines marked “A” indicate the addition of entropy into a pool; the lines marked “E” represent the extraction of entropy from an entropy pool.
On the far left side of the diagram, entropy comes from the timing of disk interrupts. Accesses to the disk generate interrupts that are unpredictable in time.
The LPNG makes a good attempt at measuring the amount of entropy it gathers. Every time a disk interrupt time sample comes into the LPNG, the amount of entropy in that sample is estimated, and that amount added to a counter in the input entropy pool. Every time that data is removed from the pool, the amount of entropy in the pool goes down. The blocking entropy pool (/dev/random) will not return any data if the amount of entropy estimated in the pool is at or below zero.
As entropy is added to a pool (the “A” lines), it is mixed into the pool using a “Twisted Generalized Feedback Shift Register” (Twisted GFSR). Think of it as a bit blender that is designed to diffuse entropy into the pool in way where no entropy is lost. Entropy is extracted from the pool (the “E” lines) by applying SHA1 over all the bits in the pool. Looking at the diagram above, there is some interesting feedback going on – every time entropy is extracted, those same bits are turned around and applied right back into the pool where they came from. Thus the pools are always changing through a combination of SHA1 and the Twisted GFSR. It sort of makes my head hurt if I think about it too hard.
Finally, the bits are made available through /dev/random and /dev/urandom. This is where openssl comes in – it reads from these to acquire seed values. We use the FIPS version of openssl, and use its default PRNG: the “CTR_DRBG” mode specified in NIST’s SP 800-90. This algorithm uses AES, and takes advantage of the fact that a good encryption algorithm (like AES) will produce ciphertext that is indistinguishable from random data. Discovering previous or future output of the CTR_DRBG mode is at least as difficult as breaking AES encryption.
Hopefully this has convinced you that we’re doing the right stuff with random numbers. The LPNG does an admirable job of processing the original entropy from disk interrupts, and the CTR_DRBG algorithm provides a secure, FIPS-approved mechanism for producing bits suitable for use as keys. As a result, our keys are strong, secure, and resistant to attacks that are possible with the NSA-backdoored DUAL_EC_DRBG random number generator.